
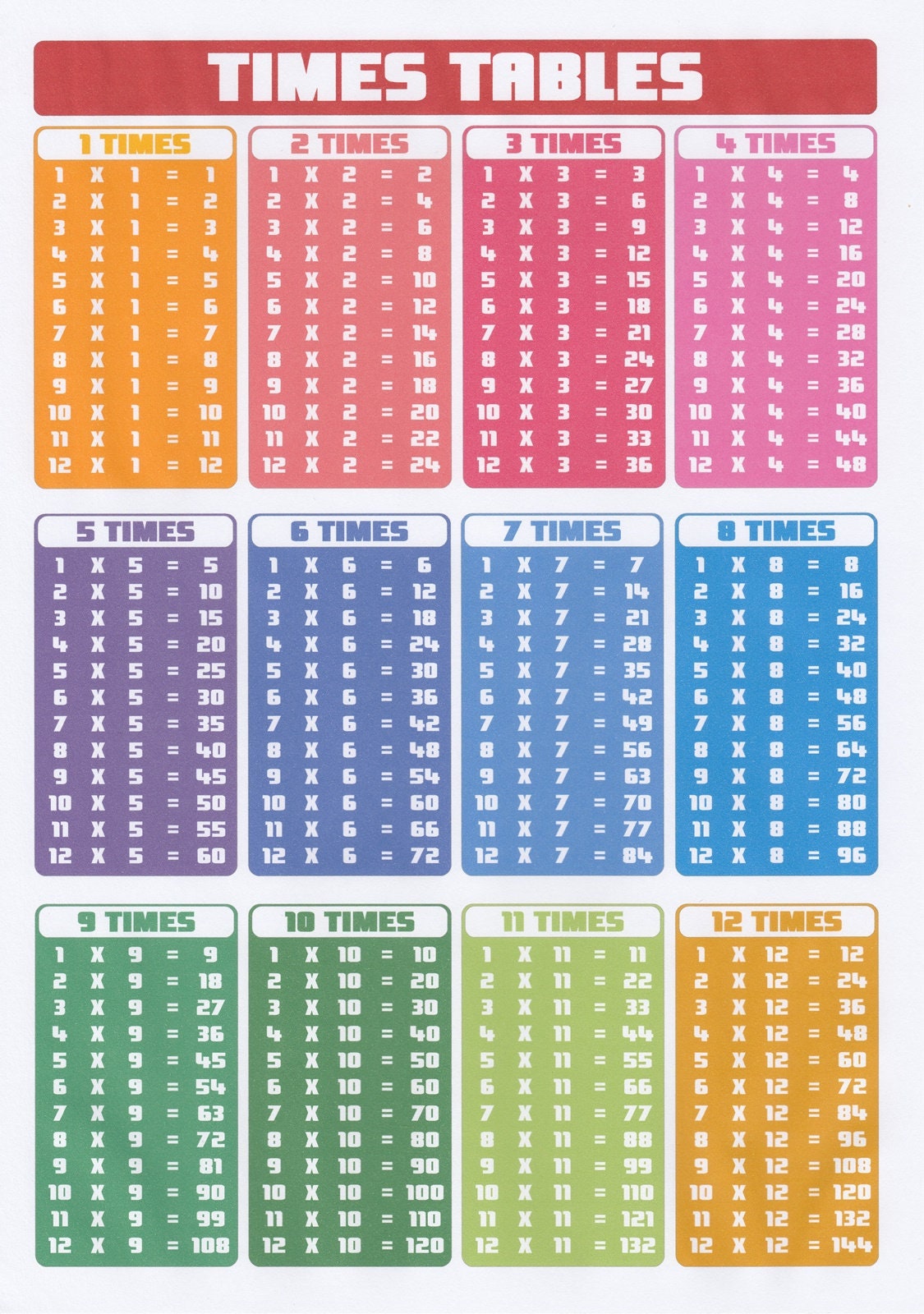
Multiples are a starting place from which to jump forward into the wonderful world of mathematical thinking. The basics are important, but they are just that, basic. Our job as mathematics educators is to create thinkers, not calculators.
Technological advances means that students need to be problem solvers, problem finders, and be flexible knowledge holders – not regurgitators of knowledge. This type of thinking does not come from rote learning multiples, it comes from understanding the concept of multiplication.Įducation has changed over the years, and teachers are great at innovating and adapting to meet the needs of both their students, and the world into which they will live. These are higher order thinking skills in relation to multiples – but this is what we are looking for when we think about being proficient in mathematics, or for students to be working mathematically. Or they might say, I could try 2 in each row, because 16 is an even number that can be counted by twos”. Students who understand multiples, should immediately be able to say “It can’t be 5 in each row, as 16 is not a multiple of 5″. A student with well-developed conceptual skills related to multiples would straight away rule out 5.

I then ask, is there another way to put the tiles in equal rows? Many students start to guess, 1, 2, 3, 5, in each row? They try these ideas out as using trial and error with the tiles, some work and others do not. I have a number sense assessment that uses the number 16, and one of the questions relates to making an array with 16 tiles: How could I divide 16 tiles into equal rows? Most students make a four x four array first. This may seem obvious, but to young children it isn’t.


 0 kommentar(er)
0 kommentar(er)
